I was prompted to write this article after receiving a catalog of tempting cycle parts that made mention of each part’s weight. Prices seemed to increase significantly for items weight just a few grams less. While it is nice to have an attractive looking cycle and this no doubt all helps with the enjoyment of what is for most of us a recreational sport, I was left wondering just how much difference a hundred grams or a few kilos actually make.
First of all we need to think of some parameters for an imaginary cyclist, so I have chosen a basic body weight of 80kg (176.37lbs) and a cycle weighing 8.5kg (18.74lbs). Our cyclist is thinking of doing a 50km sportive over a three-hour period. This particular event has 1,000m of climbing including a couple of steep sections that are 10% gradient for 500m. The cyclist, has worked out that by upgrading his wheels, pedals, handlebars, bottle carriers, and drive train that he could save as much as 500g in weight. He is wondering what difference this could make to his times.
High School Physics of Cycling
We’re going back to some high school science to find out. First, the forces acting again the cyclist that he will have to overcome. These forces include gravity, air resistance, and resistance in the drive train such as bearings, chain, and tires.
When our cyclist is moving on the flat, the amount of effort or power generated is matched by the energy dissipated in overcoming air and mechanical resistance. (I shall leave air and mechanical resistance to another article for the moment.) At a constant speed all these forces will be balanced and the cyclist will be producing energy sufficient to keep them all in balance.
Going back to our high school science the cyclist has some inherent kinetic energy due to the velocity of cycle and rider along the ground and from the rotation of the wheels:
Ke = ½ m. V2
Where m is the combined mass of the rider and cycle and V is the velocity.
Ke = ½ m.r.w2
Where m is the mass of the wheel, r is the radius and w is the rotational speed. This is actually a simplification since it depends upon how the mass of the wheel is distributed between the rim and the hub.
If the cyclist freewheels, then this kinetic energy will be dissipated to overcome air resistance and mechanical friction and they will slow down. Assuming for the moment that the cycle upgrades do not offer any advantages in aerodynamic or mechanical friction, we are left with the force of gravity that will only come into effect when going up or down hill.
The Physics of Going Downhill
What happens when we go downhill? We still have the same forces acting on the cyclist. This time, however, there is a component of the gravitational force helping him down the hill. For simplicity, we will assume that having climbed one of the steep hills, he decides to freewheel down, making use of his potential energy gained during the climb.
If you remember, the potential energy lost is:
Pe = m.G.h
Where m is the combined mass of the cyclist and cycle, G is the gravitational constant and h is the change in height.
The kinetic energy gained when he reaches the bottom is:
Ke = ½ m. V2 + ½ m.r.w2
Some energy will also be lost in overcoming air and mechanical friction, as he speeds up going down hill. Since both the Pe and Ke include the combined mass of the cyclist and rider, a change in mass will have no effect upon the velocity of the cyclist as the bottom of the hill. If you do not wish to follow the math, just remember Galileo who, it is said, dropped two different masses from the tower of Pisa in 1589 to prove they would land at the same time. So, apart from any mechanical or aerodynamic advantage, some new weight-saving parts would seem to make no difference to our cyclist’s performance on the flat or downhill.
The Physics of Going Uphill
What happens when we go uphill? To illustrate what happens in this scenario, imagine our cyclist is climbing one of the 10% gradient climbs for 500m. For simplicity, he keeps a constant speed of 10 km/h to gain 50m in height. At this speed, it takes three minutes (180 seconds) to climb the hill.
As there is no change to his speed, the kinetic energy remains constant, requiring some effort to offset air and mechanical friction. However, he has to lift his weight 50m in this time. Taking our original figures of 88.5kg for the combined weight of the cyclist and cycle, the change in potential energy will be:
Pe = 88.5 x 9.81 x 50 = 43,409 joules
Over three minutes (180 seconds) this amounts to a constant effort of 241 watts. Reducing the weight of the cycle by 500g, the amount of effort required to climb the hill at the same speed is now:
Pe = 88 x 9.81 x 50 = 43,164 joules
This amounts to a constant effort of 239 watts over three minutes, or two watts difference. Re-arranging the formulas to calculate the time taken to climb the same hill at 241 watts with a reduced weight (88kg vs. 88.5kg) gives 179 seconds, which is one second faster. Over the course of our longer ride, which has one thousand meters of climbing, this would amount to being twenty seconds faster.
The Physics of Stopping and Starting
In reality, most of my rides do not consist of constant speed sections. There are frequent changes in tempo or stops and starts. Thus, the last scenario I would like to look at is coming to a near stop and then accelerating again to a faster speed.
I am going to imagine that our cyclist accelerates on a flat surface from rest while applying 400 watts (400 joules per second) of effort, hopefully for not too long. This time, we need to look at the gain in kinetic energy required to move the rider and cycle, and rotate the wheels. The wheels and tires are assumed to have a mass of 1.5kg and a radius of 33cm.
Going back to our original equations and rearranging a few things to calculate the velocity at the end of the first second:
Ke = ½ m. V2 + ½ m.r.w2 = ½ m.(V2 + V2/r) = ½ m.(V2).(1+1/r)
V2 = Ke.2/m.r/(1+r)
V = square root of [Ke.2/m.r/(1+r)]
After the first second:
V = square root [400.2/88.5. (0.33/1.33)] = 1.5 m/s or, 5.3kph
After two seconds our rider will have supplied 800 joules and so the speed (ignoring air resistance and friction) will be 2.1m/s or 7.6kph. Note that the progression is not linear due to the square root. Continuing this process for 88.5kg and our proposed 500g weight saving gives the following table:
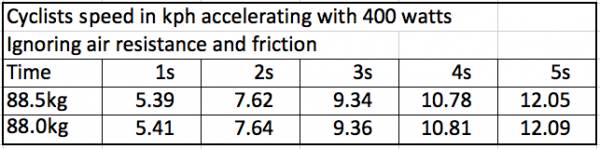
Although this has been a simplification by ignoring air resistance and friction (some of that 400 watts will be used to offset these losses as our cyclist speeds up), the gains are quite small. A weight saving of 500g would therefore give some marginal gains in accelerating and climbing. These may accumulate over the course of a longer ride with several stops and starts and significant climbs, resulting in a saved minute or two.
The Weight of the Cyclist Himself
Having looked at the cycle, now look briefly at the rider. If, having looked in the mirror one morning, the rider decides he could lose 6kg (almost a stone) of unnecessary weight, the results are a little more significant. The rider’s weight is now 74kg and the cycle stays at 8.5kg giving a combined weight of 82.5kg
Climbing the 500m 10% incline, Pe = 82.5 x 9.81 x 50 = 40,466 joules, requiring 225 watts – or sixteen watts fewer. Have you tried to improve your power output by sixteen watts? That is certainly worth saving. Keeping the power at 241 watts he would reach the top of the hill in 168 seconds – or twelve seconds sooner. Over the course of our long ride with 1000m of climbing this would be the equivalent of being four minutes faster.
In the accelerating scenario, after just a few seconds, the cyclist is almost half a kilometer per hour faster:
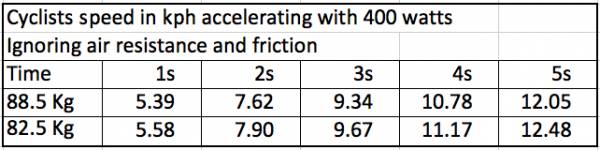
So, if you are looking at going faster with no training, sometimes it’s about the rider and not about the bike. When it comes to those fancy bike parts, you may be better off putting the wallet or purse away again.






