In my last article we covered a few of the relatively simple, but fundamental definitions that underpin sport and exercise biomechanics, relating them to the kettlebell swing.
Now, although very exciting, we didn’t really go into much detail, and detail can be important, especially when we’re talking about how we apply the forces that cause movement.
In my last article we covered a few of the relatively simple, but fundamental definitions that underpin sport and exercise biomechanics, relating them to the kettlebell swing.
Now, although very exciting, we didn’t really go into much detail, and detail can be important, especially when we’re talking about how we apply the forces that cause movement.
This article will focus on an important type of movement pattern: force-time curves, which illustrate how we apply force over time.
We’ll combine this with an explanation of Newton’s laws of motion and how they relate to the study of sport and exercise using countermovement vertical jump performance (in which the subject bends at the hips and knees before jumping). Understanding this creates a foundation for future review.
Recap: What is Force?
Recall that “… force is a pushing or pulling action that one object exerts on another.” So, if we want to move something, whether it’s barbell, kettlebell, or our own body, we have to push it or pull it – apply a force.
In the case of our jumper, force is applied to his center of mass, the point around which the masses of his segments (e.g. arms and legs) are distributed to help maintain balance.
Newton’s three laws of linear motion provide a framework of how we control movement with force, and the effect this can have on performance. Applying force to cause motion will only work if it is sufficient to overcome the inertia of the object – Newton’s first law: the law of inertia.
Inertia: It Won’t Move Itself!
Inertia is one of those words that is generally misused. In relation to Newton’s first law, inertia is the reluctance of an object to change its state, where state simply refers to whether it’s moving or not. It’s this state that is controlled by the application of force.
So, an object will remain stationary until it is pushed or pulled – force is applied. Or, once moving it will keep moving; until pushed or pulled, that is, by, you guessed it, applying a force.
But how do we control this state? The giveaway is the standard unit that inertia is reported in: the kilogram, the unit also used to report mass (well, in most of the world anyway).
This introduces perhaps the most basic type of force: weight, which is the product of mass and the acceleration of gravity. Therefore, to overcome inertia (move something) of an object we have to apply a force that exceeds its weight.
Force-Time Curves: A Basic Human Movement Pattern
From a practical perspective this is where it can get quite exciting. Human movement tends to be underpinned by the application of force to the ground through the feet (or hands, see Becca’s article on push up force).
Force platforms enable us to record these forces, and using Newton’s laws, we can manipulate them to obtain a better understanding of the mechanical demands of different types of movement (see previous article for example).
To get back on track though, Figure 1 shows the typical vertical force-time curve from vertical jump performance.
Figure 1. Typical vertical force-time curve from countermovement vertical jump performance, vertical force applied to the center of mass of our jumper.
One of the first things we tend to do to make sense of a force-time curve is determine the subject’s weight from the period of ‘quiet standing’ that can be seen in Figure 2.
In this case body weight is 787 newtons; dividing this by the acceleration of gravity (9.81) yields a body mass of just over 80 kg. We can then start thinking about applying Newton’s second law to get more information about how much force has been applied, and how much movement this will cause.
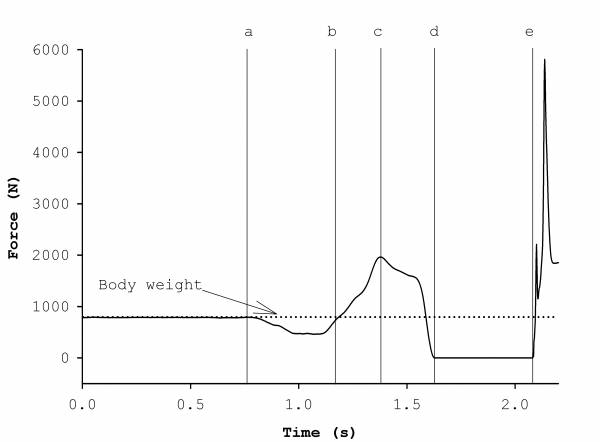
Figure 2. Annotated vertical force-time curve.
- The ‘y’ axis to point ‘a’ shows ‘quiet standing’, which is equal to the subjects’ body weight
- Point ‘a’ to ‘b’ shows ‘unweighting’ – the subject dips their knees, travelling in the same direction as the acceleration of gravity
- Point ‘b’ to ‘c’ shows the increase to peak force, where the subject slows downward movement to the lowest point of the dip
- Point ‘c’ to ‘d’ shows ‘active’ jumping (leg extension) force
- Point ‘d’ shows ‘takeoff’; points ‘d’ to ‘e’ ‘flight’ or ‘air’ time
Force, Mass, and Acceleration
Recall from the last article that force is the product of mass and acceleration (F = ma), and we can use this to decipher Figures 1 and 2.
If we know that F = ma, we can manipulate force data, like that presented in Figures 1 and 2, by dividing it by the mass of the subject, converting our force-time curve into an acceleration-time curve.
However, we need to remember Newton’s first law where we have to overcome the weight of our jumper: 787 newtons. We can simply subtract body weight from Figure 1 before dividing it by mass, which would render ‘quiet standing’ force zero.
Force would have to exceed zero to influence motion or accelerate the mass of our jumper. An example of our acceleration-time curve can be seen in Figure 3.
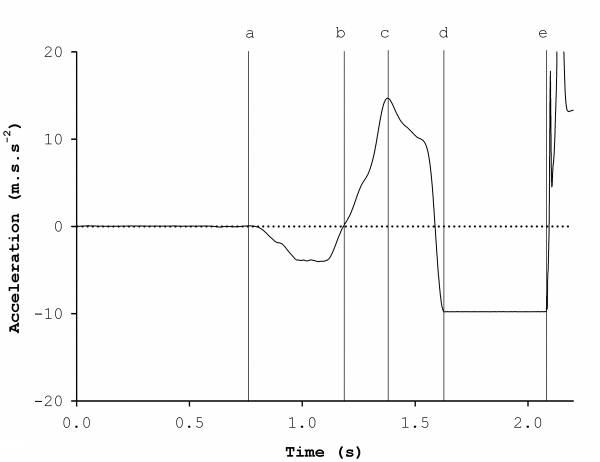
Figure 3. Annotated vertical acceleration-time curve – the acceleration of the center of mass our jumper during his jump.
This is great, but doesn’t tell us an awful lot. However, a little jiggery-pokery, in the form of some numerical integration, enables calculation of velocity – how fast our jumper moves.
Figure 4 shows velocity-time, and what are often referred to as peaks and troughs, which provide an indication of movement direction: troughs below zero indicate downward motion, peaks above zero upward motion.
We could take this a stage further and numerically integrate this velocity-time data to obtain displacement, or motion, but key measures like jump height can be quite easily obtained using equations of uniform motion.
To do this we need to determine the velocity of our jumper at takeoff, square it, then divide it by 2g (9.81 * 2), which in this case equals the following:
5.34 (2.31 [takeoff velocity2]) ÷19.62 (2g) = 27 (cm) (fairly mediocre)
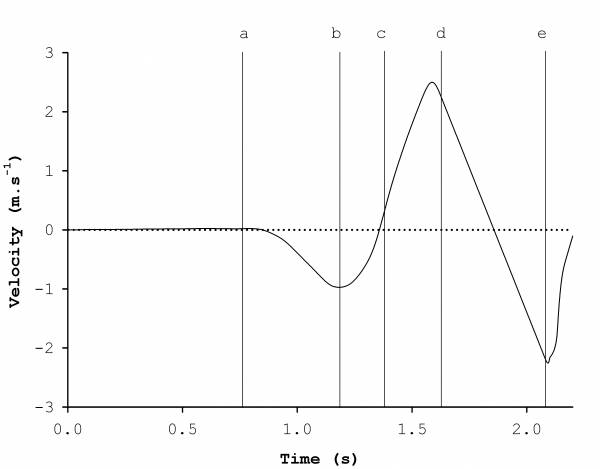
Figure 4. Annotated vertical velocity-time curve – how quickly the center of mass of our jumper is moving during his jump.
We calculate mechanical power now by multiplying our force-time data by our shiny new velocity-time data, but let’s leave this to another article, where we can do the topic justice.
Before we finish however, we should consider the practical relevance of Newton’s third law.
Action: Reaction
This is perhaps Newton’s most famous law, and it states that for every action there is an equal and opposite reaction.
Perhaps without realizing it, this law has been at work throughout our analysis in as much as if our jumper had pushed against the ground and not met an equal an opposite reaction, jump performance would have been quite tricky.
You see it’s this reaction – in combination with Newton’s second law (and friction) – that enables us to control how we move, and it seems so much easier to understand once we understand laws 1 and 2.
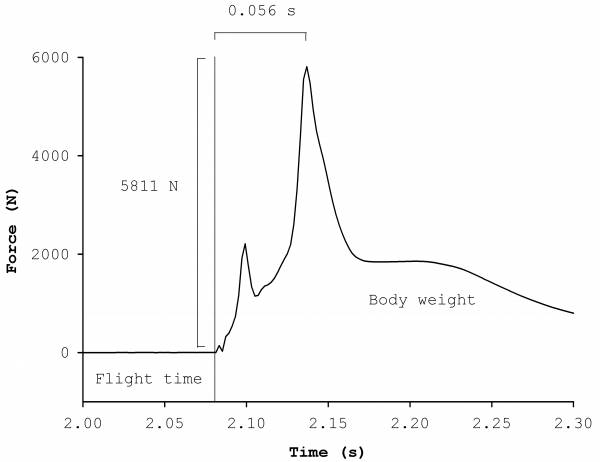
Figure 5. Forces during vertical jump landing.
The one downside to this is that it also yields a mechanical consequence. For while the reaction enables us to move, it can also act as that all-important stopping force, bringing motion to a crashing halt.
This is illustrated in Figure 5, which focuses on the change in vertical force as our jumper lands. Indeed, up to this point, our analysis has focused on the first aim of biomechanics:to improve performance, while the forces shown in Figure 5 enable us to consider the second aim of biomechanics: to minimize injury.
Identification of problem areas, like jump landing, enables us to implement technique changes to landing strategies with the aim of reducing landing force, and thus minimize injury.
Our jumper came to a halt with the help of a force equal to nearly 7.5 times his body weight. As a final thought, Figure 5 can also tell us how quickly landing force was applied to the body. In this case it was 56 milliseconds (0.056 seconds).
Dividing landing force by landing time yields something called loading rate, which in this case was just under 132 bodyweights per second – potentially problematic.
To conclude then, we can use Newton’s law of motion to manipulate force-time data to get an idea of the different phases of performance, like the vertical jump, its demands and consequences.
We’re going to use this foundation in future articles, the next of which will cover power.






